| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- laravel
- fastapi
- Redux
- 블레이드 템플릿
- nginx
- For
- SQL
- linux
- javascript
- AWS
- Backbone.js
- 기초 수학
- webpack
- Babel
- NCP
- mariadb
- deep learning
- Redis
- phpredis
- React
- php
- Machine Learning
- Go
- docker
- Node
- python
- rabbitmq
- nodejs
- Switch
- CentOS
- Today
- Total
개발일기
기초 수학 - ROC Curve와 AUC 본문

ROC(Receiver Operating Characteristic) Curve
ROC(Receiver Operating Characteristic) Curve는 이진 분류 모델의 성능을 평가하는데 사용되며 모델의 각 임계값(Threshold)에 따른 성능을 시각적으로 나타내는데 사용된다. 이전 망고 예측 예제를 예시로 아래의 표를 살펴보자. 0은 사진 속 과일이 망고가 아닌 경우고 1은 사진 속 과일이 망고인 경우를 의미한다.
| y | $ \hat y $ | 0.3 Threshold | 0.5 Threshold | 0.7 Threshold |
| 0 | 0.3 | 0(True Negative) | 0(True Negative) | 0(True Negative) |
| 1 | 0.5 | 1(True Positive) | 0(False Negative) | 0(False Negative) |
| 0 | 0.7 | 1(False Positive) | 1(False Positive) | 0(True Negative) |
임계값보다 초과의 값을 가지면 망고라고 예측한다. 예시로 임계값이 0.3이면 0.3을 초과한 0.4, 0.5, 0.6 … 의 $ \hat y $ 을 가지면 망고라고 예측한다. 반대로 0.3이하인 0.1, 0.2, 0.3의 $ \hat y $ 을 가지면 망고가 아니라고 예측한다.
$ \hat y $ 0.5를 바탕으로 위 표를 더 자세히 분석해보자.
- 임계값이 0.3일 경우 $ \hat y $ 이 이를 초과하기에 망고라고 예측한다. 망고라고 예측했고 실제로도 망고가 맞다. 예측이 맞았으며(True) 망고가 있다고(1) 예측했기 때문에(Positive) 1(True Positive)로 표시한다.
- 임계값이 0.5인 경우 $ \hat y $ 이 이를 초과하지 않기 때문에 망고가 아니라고 예측한다. 실제로는 망고가 맞으며 예측이 틀린 경우다. 예측이 틀렸으며(False) 망고가 아니라고(0) 예측했기 때문에(Negative) 0(False Negative)로 표시한다.
- 임계값이 0.7인 경우 $ \hat y $ 이 이를 초과하지 않기 대문에 망고가 아니라고 예측한다. 실제로는 망고가 맞으며 예측이 틀린 경우다. 예측이 틀렸으며(False) 망고가 아니라고(0) 예측했기 때문에(Negative) 0(False Negative)로 표시한다.
쉽게 보면 예측이 성공하면 True, 예측이 실패하면 False로 표시한다. 긍정으로 예측한 경우(존재한다) Positive로 표시하고 부정으로 예측한 경우(존재하지 않는다) Negative로 표시한다.
True Positive Rate와 False Positive Rate
위의 표를 바탕으로 True Positive Rate와 False Positive Rate를 구할 수 있다.
- True Positive Rate: 민감도(Sensitivity) 또는 재현율(Recall)이라 한다. 실제로 양성(1)인 사례 중에서 올바르게 예측한 비율을 나타낸다.
- False Positive Rate: 실제로 음성(0)인 사례 중에서 모델이 양성(1)으로 잘못 예측한 비율을 나타낸다.
TPR은 $ \frac{TP}{TP + FN} $ 로 구할 수 있다. 양성(1)이지만 음성(0)으로 예측한 것(FN)과 양성(1)을 양성(1)으로 예측한 것(TP)의 비율로 구할 수 있다.
FPR은 $ \frac{FP}{FP + TN} $ 로 구할 수 있다. 음성(0)이지만 양성(1)으로 예측한 것(TN)과 음성(0)을 음성(0)으로 예측한 것(FP)의 비율로 구할 수 있다.
위 그래프의 TPR, FPR를 구해보자.
| y | $ \hat y $ | 0.3 Threshold | 0.5 Threshold | 0.7 Threshold |
| 0 | 0.3 | 0(True Negative) | 0(True Negative) | 0(True Negative) |
| 1 | 0.5 | 1(True Positive) | 0(False Negative) | 0(False Negative) |
| 0 | 0.7 | 1(False Positive) | 1(False Positive) | 0(True Negative) |
| True Positive Rate | $ \frac{1}{1+0} = 1 $ | $ \frac{0}{0+0} = 0 $ | $ \frac{0}{0+0} = 0 $ | |
| False Positive Rate | $ \frac{1}{1+0} = 1 $ | $ \frac{1}{1+0} = 1 $ | $ \frac{0}{0+0} = 0 $ | |
TPR값은 y축에 배치하고 FPR값은 x축에 배치한 상태로 그래프를 그리면 다음과 같은 그래프가 표시된다.
# ROC Curve
import matplotlib.pyplot as plt
tpr = [1.0, 0.0, 0.0] # y
fpr = [1.0, 1.0, 0.0] # x
plt.plot(fpr, tpr, marker='o', linestyle='-', color='blue', label='ROC Curve')
plt.plot([0, 1], [0, 1], color='red', linestyle='--', label='Random Model')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()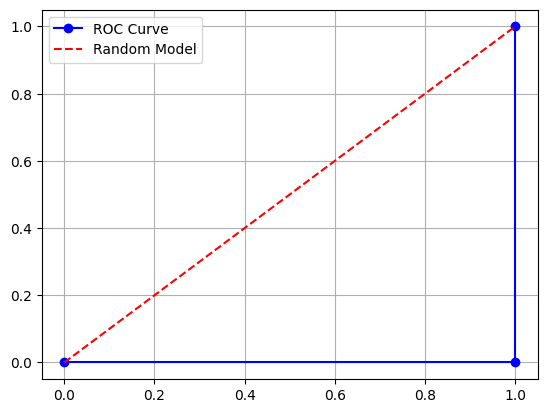
파란색은 TPR, FPR을 바탕으로 그린 그래프고 빨간 선은 무작위 예측 모델을 나타낸 그래프로 $ y = x $ 의 그래프다. 파란 선이 어느 정도 곡선을 가진채로 나와야 하는데 빨간 선 보다 아래 방향의 직각 형태로 나오고 있다. 이 모델은 성능이 매우 나쁜 모델임을 의미한다.
AUC(Area Under the Curve)
ROC Curve의 아래 면적을 AUC(Area Under the Curve)라고 하며 이 값을 통해 모델의 성능을 간단하게 요약해준다.
- AUC = 1: 완벽한 모델
- AUC = 0.5: 무작위 예측 모델(무작위이기 때문에 성능이 없음 - 빨간 선)
- AUC < 0.5: 무작위 모델보다 성능이 안 좋은 매우 나쁜 모델(파란 선)
AUC 면적을 구하는데 적분이 사용되는데 현재 모델로는 적분 값을 구할 수 없기에 약간의 TPR, FPR 변형을 통해 그래프를 변경할 수 있다.
# ROC Curve
import matplotlib.pyplot as plt
tpr = [1.0, 0.0, 0.0] # y
fpr = [1.0, 1.0, 0.0] # x
# NEW ROC Curve
n_tpr = [0.0, 0.5, 0.5, 1.0, 1.0] # y
n_fpr = [0.0, 0.0, 0.5, 0.5, 1.0] # x
plt.plot(fpr, tpr, marker='o', linestyle='-', color='blue', label='ROC Curve')
plt.plot(n_fpr, n_tpr, marker='o', linestyle='-', color='green', label='New ROC Curve')
plt.plot([0, 1], [0, 1], color='red', linestyle='--', label='Random Model')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()
초록 그래프는 새로운 ROC Curve 그래프다. 직관적으로 보면 이 그래프의 AUC 값이 0.75 인 것을 짐작할 수 있다.
- AUC 0.75: 초록색
- AUC 0.5: 빨간색
- AUC 0: 파란색
AUC 구하기
AUC 값은 sklearn의 auc을 통해 구할 수 있다.
# AUC
from sklearn.metrics import auc
n_tpr = [0.0, 0.5, 0.5, 1.0, 1.0] # y
n_fpr = [0.0, 0.0, 0.5, 0.5, 1.0] # x
auc_value = auc(n_fpr, n_tpr)
print(auc_value)
# 0.75
auc(): 첫번째 파라미터는 x축 값을 넣고 두번째 파라미터에는 y축 값을 대입하여 AUC를 구할 수 있다.
모델 성능 측정
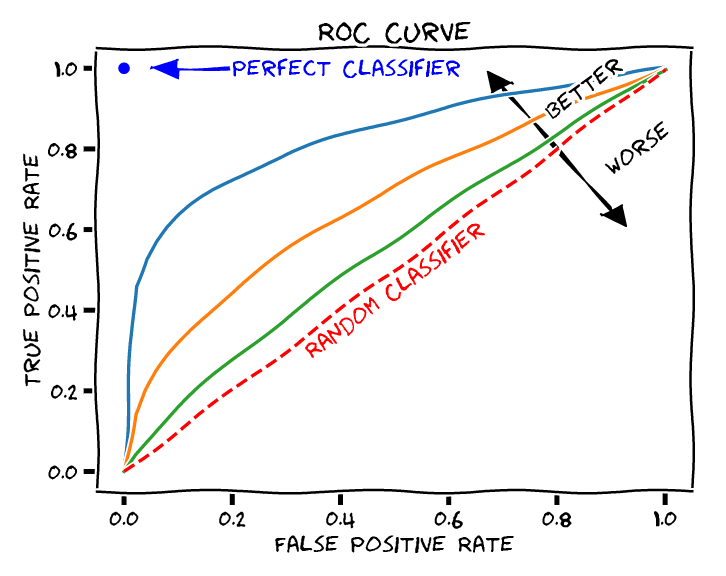
ROC Curve에 따른 AUC 면적은 위의 사진을 토대로 파란 점으로 수렴할수록 좋은 모델임을 의미한다. 적어도 최소한 빨간 선 윗부분의 면적을 차지하면 괜찮은 성능을 의미하며 그 밑 부분은 나쁜 성능을 가진 모델이란 것을 의미한다.
참고 사이트:
A Gentle Introduction to ROC Curve and AUC in Machine Learning - Sefik Ilkin Serengil (sefiks.com)
A Gentle Introduction to ROC Curve and AUC in Machine Learning - Sefik Ilkin Serengil
ROC Curves and AUC score are one of the most common way for classification problems. We'll mention why we need those explainers in a timeline
sefiks.com
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.auc.html
auc
Gallery examples: Species distribution modeling Poisson regression and non-normal loss Tweedie regression on insurance claims Multiclass Receiver Operating Characteristic (ROC) Precision-Recall Rec...
scikit-learn.org
https://colab.research.google.com/drive/1JGDupyKe0KKRUQnSCSJ-PTdQRTWet19r?usp=sharing
ROC Curve, AUC.ipynb
Colab notebook
colab.research.google.com
https://phsun102.tistory.com/183
기초 수학 - 혼동 행렬(The Confusion Matrix)
혼동 행렬(The Confusion Matrix)는 이진 분류 모델의 성능을 평가하는데 사용되며 예측 결과와 실제 결과의 차이를 비교하여 시각적으로 표현한 2x2 행렬을 의미한다. 혼동 행렬이라 불리는 이유는 알
phsun102.tistory.com
https://phsun102.tistory.com/182
기초 수학 - 적분(Integration)의 개념(부정 적분, 정적분)
머신 러닝에서 적분(Integration)이란?적분은 함수의 넓이, 부피, 길이 등을 계산하는데 사용되는 개념으로 머신 러닝에서는 함수 그래프의 곡선 아래 영역에 대한 내용을 다룬다. 머신 러닝에서 적
phsun102.tistory.com
https://www.buymeacoffee.com/flashback_music
Flashback
Hi, I'm a programmer and like to play games. :D
buymeacoffee.com
'AI > 기초 수학' 카테고리의 다른 글
| 기초 수학 - 시그모이드(Sigmoid) 함수 (0) | 2024.10.11 |
|---|---|
| 기초 수학 - 데이터 정규화(Data Normalization) (0) | 2024.07.20 |
| 기초 수학 - 혼동 행렬(The Confusion Matrix) (0) | 2024.07.15 |
| 기초 수학 - 적분(Integration)의 개념(부정 적분, 정적분) (0) | 2024.07.14 |
| 기초 수학 - 편미분과 선형 회귀 모델 응용 (0) | 2024.07.07 |




