| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- nodejs
- linux
- Node
- fastapi
- nginx
- php
- AWS
- docker
- python
- javascript
- Switch
- deep learning
- For
- 블레이드 템플릿
- laravel
- Backbone.js
- webpack
- Babel
- Machine Learning
- React
- Go
- rabbitmq
- 기초 수학
- Redux
- mariadb
- SQL
- Redis
- NCP
- CentOS
- phpredis
- Today
- Total
개발일기
기초 수학 - 시그모이드(Sigmoid) 함수 본문

Sigmoid 함수
sigmoid 함수는 입력값을 0과 1사이의 값으로 변환하는 비선형 함수로 주로 이진 분류 문제에서 확률을 계산하여 참, 거짓을 판단하기 위해 사용된다. 출력값의 범위가 0과 1사이에 있으며 0%~100%와 같이 확률적인 의미로 표현될 수 있다. 만약 함수의 출력값이 0.9라면 해당 입력이 참(1에 수렴하는)에 속할 확률이 90%인 것을 의미한다. 이와 반대로 출력값이 0.2라면 거짓(0에 수렴하는)에 속할 확률이 80%라는 것을 의미한다. 또한 sigmoid 함수는 비선형 함수이기 때문에 0과 1 주변에서는 기울기가 완만한 S자 모양의 그래프를 가진다.
수학 수식으로는 $ \sigma(x) = \frac{1}{1 + e^{-x}} $로 표현한다.
- $ sigma(x) $: $ \sigma $ 는 sigmoid 함수라는 것을 의미한다. $ (x) $ 는 $ \sigma $ 의 입력값이 x라는 것을 의미한다.
- $ e^{-x} $: $ e $ 는 자연 상수를 의미하며 대략 2.718의 값을 가진다. $ e^{-x} $ 는 지수 함수로 $ x $ 가 양수면 $ e^{-x} $ 가 작아지고, 반대로 $ x $ 가 음수면 $ e^{-x} $ 의 값이 커진다. 이 부분이 sigmoid 함수의 핵심 부분으로 이 식이 함수의 비선형성을 담당한다.
- 분수: 입력값을 비선형적으로 변환하여 출력하기 때문에 sigmoid함수는 분자에 1, 분모에 $ 1 + e^{-x} $ 가 위치한다. 이러한 분수 구조로 인해 입력값의 크기에 따라 출력값이 1 또는 0에 가까워진다.
일반적으로 입력값이 크면 출력값이 0에 수렴하게 된다. 이와 반대로 입력값이 작으면 출력값이 1에 수렴하게 된다.
import numpy as np
def sigmoid(x): # Sigmoid 함수
return 1 / (1 + np.exp(-x)) # exp는 지수 함수를 의미함
x_positive = sigmoid(10) # 입력값이 양수(입력값이 큰경우)
x_negative = sigmoid(-10) # 입력값이 음수(입력값이 작은경우)
x_zero = sigmoid(0) # 입력값이 0
print('x양수: ', x_positive)
print('x0: ', x_zero)
print('x음수: ', x_negative)
"""
x양수: 0.9999546021312976
x0: 0.5
x음수: 4.5397868702434395e-05
"""sigmoid 함수를 파이썬으로 만든 후, 입력값에 양수, 음수, 0을 넣고 출력하면 위와 같은 값이 출력된다. 상대적으로 큰 값인 양수 10을 입력하면 1에 수렴하는 값이 출력되는 것을 확인할 수 있다. 음수 부분은 얼핏보며 4.5... 로 볼 수 있지만 뒤에 e-05가 붙는다. 이는 지수 표기법으로 $ 10^{-5} $ 를 의미한다. 이를 환산하면 소수점이 4개가 추가된 0.00004539...로 0에 수렴하는 값을 가진다.
특이하게 0을 입력하면 0과 1의 중앙값인 0.5가 출력된다. 수학 수식으로 표현하면 $ \sigma(0) = \frac{1}{1 + e^{0}} = \frac{1}{1 + 1} = \frac{1}{2} = 0.5 $ 가 된다. 이는 sigmoid 함수의 대칭성으로 인한 결과이며 x가 음수면 출력값은 0에 가까워 지고 양수면 1에 가까워 지는 대칭성으로 인해 이 양수도 아니고 음수도 아닌 0이 입력되면 중앙값인 0과 1의 중앙값 0.5가 출력되게 된다.
import numpy as np
import matplotlib.pyplot as plt
# sigmoid function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# x range: -10 ~ 10
x_values = np.linspace(-10, 10, 1000)
y_values = sigmoid(x_values)
# Visualization
plt.plot(x_values, y_values, color='blue')
plt.xlabel('$ x $')
plt.ylabel('$ \\sigma(x) $')
plt.grid(True)
plt.axhline(0.5, color='red', linestyle='--', linewidth=0.7) # 0.5 중앙값
plt.show()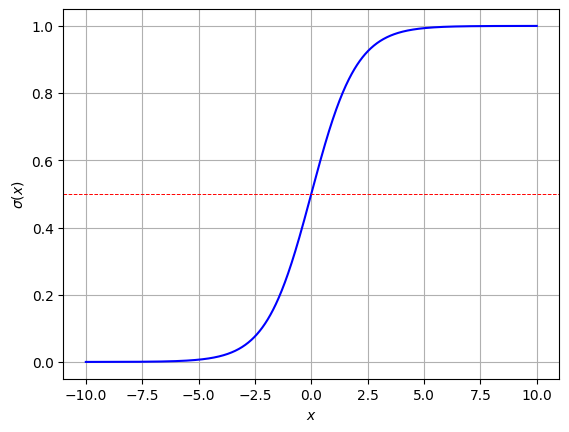
sigmoid 함수를 그래프로 표시하면 위와 같이 0과 1에 수렴하는 S모양의 그래프가 나타난다.
이러한 sigmoid 함수는 로지스틱 회귀와 신경망 활성화 함수에 사용된다. 로지스틱 회귀 모델은 데이터를 바탕으로 두 가지 범주 중에서 하나에 속할 확률을 예측하는 회귀 분석 방식이다. 이때 sigmoid 함수를 활용하여 입력값을 0과 1 사이의 값으로 변환하는 역할을 한다. 이를 통해 이진 분류 문제에서 각 범주의 확률을 예측할 수 있다.
하지만 이러한 sigmoid함수에는 기울기 소실 문제(Vanishing Gradient)라는 문제가 존재한다. 이는 딥러닝 모델에서 발생하는 sigmoid 함수의 한계점이다. 입력값이 극단적으로 크거나 작을 경우 출력값이 1 또는 0에 매우 가까워진다. 이로 인해 미분값이 0에 가까워지며 역전파 알고리즘에서 기울기가 소실되어 학습이 제대로 이루어지지 않는 문제가 발생한다. 이로 인해 대부분의 딥러닝 모델에서는 ReLU 활성화 함수를 사용하여 sigmoid 함수의 문제점을 보완하여 사용하고 있다.
참고 사이트:
https://www.digitalocean.com/community/tutorials/sigmoid-activation-function-python
The Sigmoid Activation Function - Python Implementation | DigitalOcean
While we believe that this content benefits our community, we have not yet thoroughly reviewed it. If you have any suggestions for improvements, please let us know by clicking the “report an issue“ button at the bottom of the tutorial.
www.digitalocean.com
https://machinelearningmastery.com/a-gentle-introduction-to-sigmoid-function/
'AI > 기초 수학' 카테고리의 다른 글
| 기초 수학 - 합성곱(Convolution) 연산 (0) | 2024.12.25 |
|---|---|
| 기초 수학 - 데이터 정규화(Data Normalization) (0) | 2024.07.20 |
| 기초 수학 - ROC Curve와 AUC (0) | 2024.07.15 |
| 기초 수학 - 혼동 행렬(The Confusion Matrix) (0) | 2024.07.15 |
| 기초 수학 - 적분(Integration)의 개념(부정 적분, 정적분) (0) | 2024.07.14 |




