| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- phpredis
- CentOS
- php
- fastapi
- Babel
- React
- javascript
- nginx
- Redis
- deep learning
- Backbone.js
- SQL
- Redux
- 블레이드 템플릿
- mariadb
- laravel
- python
- docker
- rabbitmq
- For
- webpack
- Node
- NCP
- nodejs
- linux
- 기초 수학
- Machine Learning
- Go
- Switch
- AWS
- Today
- Total
개발일기
머신 러닝 - California Housing Price Prediction(Regression) 본문
머신 러닝 - California Housing Price Prediction(Regression)
Flashback 2024. 8. 18. 17:49
Sklearn에서 제공하는 캘리포니아 집값 예측 데이터셋을 선형 회귀 모델로 학습시키면 각 특성과 주택 가격 간의 연관성을 파악할 수 있다. 선형 회귀 모델은 훈련 데이터에 대한 손실 함수를 최소화하여 가중치와 절편을 찾는 과정을 통해 학습한다. 주로 사용하는 손실 함수는 평균 제곱 오차(MSE)이며 훈련 데이터에 존재하는 특성에 대한 가중치를 구해 집값에 영향을 미치는 정도를 확인할 수 있다.
데이터셋 확인
# Pytorch California Housing
from sklearn.datasets import fetch_california_housing
# Load the California housing dataset
housing = fetch_california_housing(as_frame=True)
# as_frame=True: Pandas data frame
# as_frame=False: numpy data frame
housing = housing.frame
housing.head()
- fetch_california_housing(): import된 캘리포니아 집값 훈련 데이터를 가져온다. 파라미터에 as_frame을 True로 설정하면 data와 target을 pandas dataframe 형식으로 데이터를 가져온다. as_frame을 False로 설정하면 numpy 형식으로 데이터를 가져온다.
- frame: 데이터 프레임을 볼 수 있게 해준다. as_frame=True로 설정하지 않으면 해당 데이터 프레임이 존재하지 않는다.
- head(): 데이터 프레임의 상위 5개 행을 출력한다.
데이터 특성 확인
frame, head()를 활용하여 상위 5개 행의 데이터가 출력되며 이 표를 통해 데이터의 특성과 대략적인 데이터를 알 수 있다. 데이터 특성의 종류는 MedInc(중위 소득), Housing Age(주택 연식), AveRooms(평균 방 개수), AveBedrms(평균 침실 수), Population(인구 수), AveOccup(평균 거주자 수), Latitude(위도), Longitude(경도)로 총 8개의 특성을 가지고 있다.
# Data Info: Column, Non-Null Count, Dtype
housing.info()
"""
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 MedInc 20640 non-null float64
1 HouseAge 20640 non-null float64
2 AveRooms 20640 non-null float64
3 AveBedrms 20640 non-null float64
4 Population 20640 non-null float64
5 AveOccup 20640 non-null float64
6 Latitude 20640 non-null float64
7 Longitude 20640 non-null float64
8 MedHouseVal 20640 non-null float64
dtypes: float64(9)
memory usage: 1.4 MB
"""
info(): frame과는 다르게 칼럼명과 데이터 타입을 보여준다. 또한 Null 또는 NaN이 아닌 값의 수를 표시한다. Null, Nan은 결측값으로 데이터셋에 누락된 데이터를 나타낸다.
히스토그램
각 특성에 따른 데이터의 분포를 히스토그램을 통해 확인하여 대략적으로 데이터를 분석할 수 있다.
# Data Histogram
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(12,8))
plt.show()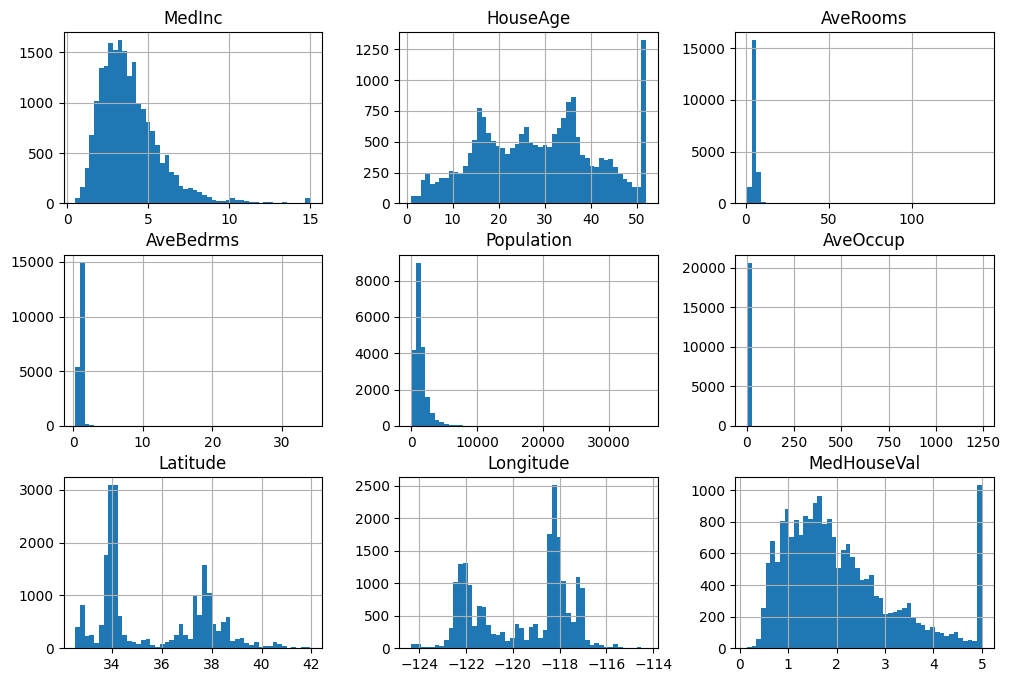
- bins: 히스토그램의 세밀도를 조절할 수 있는 옵션이다. bins의 수를 늘리면 더 넓은 범위로 볼 수 있어 전반적인 분포를 확인할 수 있으며 bin의 수를 줄이면 더 세밀하게 분석할 수 있다.
상관관계 분석
데이터의 분포 이외에도 데이터 특성들과 타겟 데이터인 집값과의 상관 관계를 분석할 수 있다. 상관 관계를 나타내는 상관 계수가 높으면 두 변수에 강한 연관성이 있다고 판단할 수 있다.
# 상관 관계 매트릭스 시각화
import pandas as pd
import seaborn as sns
housing = fetch_california_housing()
data = pd.DataFrame(housing.data, columns=housing.feature_names) # 컬럼명: 데이터 특징 이름
data['MedHouseVal'] = housing.target # 타겟 데이터: MedHouseVal
corr_matrix = data.corr() #
plt.figure(figsize=(12, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f', linewidths=0.5) # 히트맵 표시
plt.title('Correlation Matrix')
plt.show()
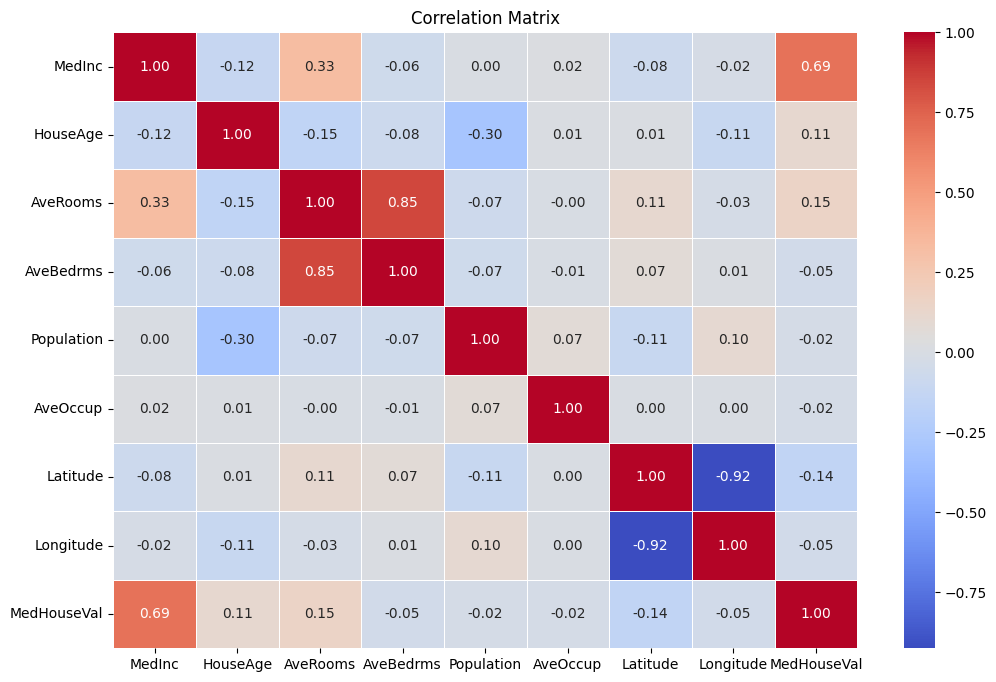
- corr(): pandas 프레임으로 된 데이터에서 각 열 간의 상관 관계를 반환하는 메서드다.
- sns.heatmap(): 상관 관계를 바탕으로 히트맵을 출력해준다. 히트맵은 corr_matrix에 속해있는 상관 관계를 열의 농도를 통해 표현한다.
히트맵을 보면 MedInc(중위 소득)와 MedHouseVal(한 구역 내의 주택 중앙값)이 0.69로 표시되며 높은 상관 관계를 가진 것을 확인할 수 있다. AveRooms와 AveBedrms는 0.85로 더 높은 상관 관계를 가지고 있지만 이 모델의 목표 변수는 MedHouseVal이기 때문에 MedHouseVal과의 상관 관계를 비교해야 한다.
히트맵과 히스토그램을 통해 특성별 데이터의 전반적인 분포를 확인할 수 있으며 이상치(Outliers)를 탐지하거나 데이터가 한쪽으로 치우쳐 있는 데이터 왜곡의 정도를 파악할 수 있다.
- 이상치: 데이터가 일정 범위에서 벗어나 극단적으로 분포되어 있는 데이터를 의미한다.
- 데이터 왜곡: 데이터가 평균을 기준으로 비대칭적이며 한쪽으로 치우쳐 있는 상태를 의미한다.
데이터 히스토그램을 통해 HouseAge와 MedHouseVal에 왜곡이 존재한다는 것을 확인할 수 있다. HouseAge는 50년 이상된 주택을 모두 x 50에 표시되어 있으며 MedHouseVal은 $500,000 이상일 경우 모두 x 5에 표시되고 있다. 즉 두 특성의 데이터는 오른쪽으로 치우쳐 분포되어 있다. MedInc와 MedHouseVal 사이의 상관 관계가 높은 편이기 때문에 MedInc 데이터의 이상치로 인해 MedHouseVal 데이터의 이상치로 연결되었을 가능성이 크다.
이상치 제거
이러한 데이터 왜곡은 두 특성 데이터에 이상치가 존재하기 때문에 데이터 왜곡이 발생한다. 이상치를 제거하기 위해선 먼저 Box Plot형태로 이상치의 존재 유무를 시각화한다. 그 후, 정규 분포 안에 존재하는 이상치는 IQR 또는 Z-Score를 통해 이상치를 제거한다.
import numpy as np
housing = fetch_california_housing(as_frame=True)
# as_frame=True: Pandas data frame
# as_frame=False: numpy data frame
housing = housing.frame
def iqr_outliers():
global housing
list_of_masks_for_outlier_removal = []
outliers_list = ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup'] # 이상치를 파악한 특성 목록
for i, item in enumerate(outliers_list):
Q1, Q3 = np.percentile(housing[item], [25, 75]) # Q1: 하위 25%, Q3: 상위 25%
IQR = Q3 - Q1 # 상위 25% 와 하위 25% 사이의 범위
lower_bound = Q1 - 1.5 * IQR # IQR 하한선
upper_bound = Q3 + 1.5 * IQR # IQR 상한선
lower_data = housing[item] >= lower_bound
upper_data = housing[item] <= upper_bound
outliers = len(housing[(housing[item] < lower_bound) | (housing[item] > upper_bound)])
print(f'{item}: {outliers}')
housing = housing[lower_data & upper_data] # 이상치 제거
iqr_outliers()
print(f'After Remove Outliers: {housing.shape}')
"""
MedInc: 681
HouseAge: 0
AveRooms: 439
AveBedrms: 1116
Population: 1063
AveOccup: 528
After Remove Outliers: (16813, 9)
"""from scipy import stats
def z_score_outliers():
global housing
features = housing.drop(columns=['MedHouseVal', 'Longitude', 'Latitude'])
z_scores = np.abs(stats.zscore(features))
threshold = 3
outliers = (z_scores > threshold).any(axis=1)
print('Z-Score Outliers Count: ', outliers.sum())
housing = housing.loc[~outliers]
z_score_outliers()이상치를 제거한 후, 예제 데이터를 학습과 테스트를 위해 적당한 양으로 분할한다. IQR과 Z Score 중에서 IQR로 이상치를 제거한 후 실행한 코드이다.
from sklearn.model_selection import train_test_split
x = housing.drop(columns=['MedHouseVal']) # 입력 데이터 (특성) - MedHouseVal을 제외한 모든 특성
y = housing['MedHouseVal'] # 출력 데이터 (타겟)
# 훈련 데이터와 테스트 데이터로 분할
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)- train_test_split(): 데이터를 훈련용과 테스트용으로 분할하기 위해 사용하는 함수다.
- x_train, x_test, y_train, y_test: 뒤에 train이 붙으면 학습용 데이터, 뒤에 test가 붙으면 테스트용 데이터란 의미다.
- test_size: 0.2로 설정되어 있으며 20%는 테스트용, 나머지 80%는 학습용으로 사용하겠다는 비율을 나타낸다. 0.3으로 설정하면 30%는 테스트용 데이터가 되며 나머지 70%는 학습용 데이터가 된다. 0.2로 설정한 이유는 일반적으로 사용되는 비율 중 하나이며 80%의 학습용 데이터로도 충분히 학습을 할 수 있기 때문에 0.2로 설정하였다.
- random_state: 데이터 분할에 랜덤성을 부여하기 위해 사용하는 파라미터다. random_state에 값을 지정하면 데이터를 같은 방식으로 분할하여 동일하게 초기화 시킬 수 있다. 즉, random_state를 42로 지정하고 한 번 실행, 두번 실행 또는 세번 실행했을 때 모두 동일한 분할 결과를 얻을 수 있다. 하지만 random_state를 16과 같이 다르게 변경하면 42와는 다른 분할 결과를 얻을 수 있다. 즉 random_state가 고정되면 매 실행마다 동일한 분할 결과를 바탕으로 일관적인 출력 데이터로 테스트 시 유용하게 사용할 수 있다.random_state를 아예 지정하지 않으면 매 실행마다 랜덤하게 분할된다. 이를 바탕으로 random_state를 Boolean형으로 하여 True, False로 지정하면 어떨까라고 생각을 할 수도 있지만 만약 random_state가 Boolean형이라면 랜덤 여부의 분기점 역할을 하게 될 것이다. 즉 분기점 역할은 넘어서 랜덤성에 무작위를 부여하기 위해 random_state는 Integer 형으로 이루어져 있는 것이다.
- 42로 지정하는 이유는 관습적인 이유이며 Douglas Adams의 소설 ‘The Hitchhikers’ Guide to the Galaxy의 “Answer to the Ultimate Question of Life, the Universe, and Everything”라는 질문의 대답인 42에서 유래했다고 한다.
test_size에 따른 x, y 데이터의 분할 결과를 shape를 사용하여 확인할 수 있다.
print('x 입력 데이터:', x.shape) # input data
print('y 목표 데이터: ', y.shape) # target data
print('x 학습용: ', x_train.shape) # train data
print('x 테스트용: ', x_test.shape) # test data
print('y 학습용: ', y_train.shape) # train data
print('y 테스트용', y_test.shape) # test data shape...
"""
x 입력 데이터: (16813, 8)
y 목표 데이터: (16813,)
x 학습용: (13450, 8)
x 테스트용: (3363, 8)
y 학습용: (13450,)
y 테스트용 (3363,)
"""목표 데이터 y는 특성이 없고 집값이라는 하나의 데이터만 존재하기에 1차원 베열로 이루어져 있다.
데이터 정규화
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)- StandardScaler(): sklearn에서 제공하는 Z Socre 정규화 클래스다.
- fit_transform: 훈련 데이터를 학습하고 동시에 정규화를 진행한다. 단계는 크게 1. fit, 2. transform으로 나뉜다. 먼저 fit단계에서는 평균(mean)과 표준 편차(std)를 구한 후, transform 단계에서 정규화를 진행한다. 주로 훈련용 데이터에 사용한다.
- transform: x_train데이터에서 데이터의 평균과 표준 편차를 구했기 때문에 fit과정없이 바로 정규화를 진행한다. 주로 테스트용 데이터에 사용한다.
데이터의 규모가 각 특성마다 다르기 때문에 정규화를 통해 데이터의 특성 값을 일정한 비율로 조절한다. 서로 다른 특성들이 비슷한 규모의 값 범위를 가지면 모델의 성능이 향상되며 안정적인 학습이 가능해진다.
회귀 분석
California Housing모델을 여러개의 회귀 분석을 통해 학습을 진행할 수 있다. 회귀 분석의 종류에는 Linear Regression, Ridge Regression, Lasso Regression, Decision Tree Regression, Random Forest Regreession, Gradient Boosting Regression, XGBoost Regression 등이 있다.
# Performance Metrics
data_mse = {} # MSE 평가 지표
data_score = {} # R2 Score 평가 지표
각 모델의 성능 평가 지표로 mse, r2 score를 사용한다.
# Linear Regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
def linear_regression_model():
# Create Model and Fit
model = LinearRegression()
model.fit(x_train, y_train)
# Model Prediction
y_pred = model.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
data_mse['linear_regression'] = mse
# Performance Metrics: R2 Score
data_score['linear_regression'] = r2_score(y_test, y_pred)
# Ridge Regression
from sklearn.linear_model import Ridge
def ridge_regression():
# Create Model and Fit
ridge_reg = Ridge(alpha=1.0)
ridge_reg.fit(x_train, y_train)
# Model Prediction
y_pred = ridge_reg.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
data_mse['ridge_regression'] = mse
# Performance Metrics: R2 Score
score = r2_score(y_test, y_pred)
data_score['ridge_regression'] = score
# Lasso Regression
from sklearn.linear_model import Lasso
def lasso_regression():
# Create Model and Fit
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(x_train, y_train)
# Model Prediction
y_pred = lasso_reg.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
data_mse['lasso_regression'] = mse
# Performance Metrics: R2 Score
score = r2_score(y_test, y_pred)
data_score['lasso_regression'] = score
# Decision Tree Regression
from sklearn.tree import DecisionTreeRegressor
def decision_tree_regression():
# Create Model and Fit
tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(x_train, y_train) # 트리 기반 모델은 스케일링이 필요하지 않음
# Model Prediction
y_pred = tree_reg.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
data_mse['decision_tree_regression'] = mse
# Performance Metrics: R2 Score
score = r2_score(y_test, y_pred)
data_score['decision_tree_regression'] = score
# Random Forest Regreession
from sklearn.ensemble import RandomForestRegressor
def random_forest_regression():
# Create Model and Fit
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
forest_reg.fit(x_train, y_train) # 트리 기반 모델은 스케일링이 필요하지 않음
# Model Prediction
y_pred = forest_reg.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
score = r2_score(y_test, y_pred)
# Performance Metrics: R2 Score
data_mse['random_forest_regression'] = mse
data_score['random_forest_regression'] = score# Gradient Boosting Regression
from sklearn.ensemble import GradientBoostingRegressor
def gradient_boostring_regression():
# Create Model and Fit
boostring_reg = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
boostring_reg.fit(x_train, y_train)
# Model Prediction
y_pred = boostring_reg.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
data_mse['gradeint_boosting_regression'] = mse
# Performance Metrics: R2 Score
score = r2_score(y_test, y_pred)
data_score['gradeint_boosting_regression'] = scorefrom xgboost import XGBRegressor
def xgboost_regression():
# Create Model and Fit
model = XGBRegressor(objective='reg:squarederror', n_estimators=100, learning_rate=0.1, random_state=42)
model.fit(x_train, y_train)
# Model Prediction
y_pred = model.predict(x_test)
# Performance Metrics: MSE
mse = mean_squared_error(y_test, y_pred)
data_mse['xgboost_regression'] = mse
# Performance Metrics: R2 Score
score = r2_score(y_test, y_pred)
data_score['xgboost_regression'] = score# Regression Test
y_pred = xgboost_regression()
res_data = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})
res_data['Error'] = res_data['Actual'] - res_data['Predicted']
print(res_data.head(20)) # 첫 20개 행에서 데이터와 오차 확인
print('MSE: ', data_mse)
print('R2 Score: ', data_score)
"""
Actual Predicted Error
53 1.04200 1.008007 0.033993
2059 0.65300 0.881210 -0.228210
3204 0.90600 1.419763 -0.513763
1303 1.00000 1.178101 -0.178101
13632 0.90500 0.790896 0.114104
5732 3.75700 4.226183 -0.469183
12796 0.51700 0.696159 -0.179159
11016 2.65600 3.118364 -0.462364
17280 2.61000 2.504808 0.105192
13907 0.84000 0.980654 -0.140654
11839 0.83500 0.870769 -0.035769
10994 2.25000 2.345470 -0.095470
4679 5.00001 4.852245 0.147765
9889 1.54600 1.720023 -0.174023
3735 2.61800 2.491754 0.126246
2313 0.86300 0.862198 0.000802
14556 3.37000 3.537022 -0.167022
14276 0.80200 0.906833 -0.104833
13589 0.63500 0.778713 -0.143713
9173 2.85200 2.389820 0.462180
MSE: {'xgboost_regression': 0.19870779757756105}
R2 Score: {'xgboost_regression': 0.8297524535249905}
"""회귀 모델들 중에서 XGBoost Regression가 가장 좋은 성능을 보인다. 다른 회귀 방식과 비교했을 때, 오차가 낮고 실제 값이 근접한 값을 예측해 내는 것을 확인할 수 있으며 평가 지표인 MSE와 R2 Score값도 확인할 수 있다. 일반적으로 MSE값은 낮고 R2 Score는 높아야 좋은 모델로 평가된다.
최종 코드
# Final Result
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
housing = fetch_california_housing(as_frame=True)
housing = housing.frame
# 이상치 제거
# iqr_outliers()
# z_score_outliers()
# Select Outlier Option
# 훈련 데이터와 테스트 데이터로 분할
x = housing.drop(columns=['MedHouseVal']) # 입력 데이터 (특성) - MedHouseVal을 제외한 모든 특성
y = housing['MedHouseVal'] # 출력 데이터 (타겟)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
# 정규화
scaler = StandardScaler() # Z Score 정규화
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
# Performance Metrics
data_mse = {} # MSE 평가 지표
data_score = {} # R2 Score 평가 지표
# 결과 확인
# y_pred = linear_regression_model()
# y_pred = ridge_regression()
# y_pred = lasso_regression()
# y_pred = decision_tree_regression()
# y_pred = random_forest_regression()
# y_pred = gradient_boostring_regression()
# y_pred = xgboost_regression()
# Select Regression Option
res_data = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})
res_data['Error'] = res_data['Actual'] - res_data['Predicted']
print(res_data.head(20)) # 첫 20개 행에서 데이터와 오차 확인
print('MSE: ', data_mse)
print('R2 Score: ', data_score)
참고 사이트:
https://colab.research.google.com/drive/1_06eKHCvn4EjuU-UNUUHjCgUYph5Gtw0?usp=sharing
California Housing - Regression.ipynb
Colab notebook
colab.research.google.com
Implementing Linear Regression on California Housing Dataset
In this article, I will walk you through basic linear regression implementation using python scikit-learn.
medium.com
What is "random-state" in sklearn.model_selection.train_test_split example?
Can someone explain me what random_state means in below example? import numpy as np from sklearn.model_selection import train_test_split X, y = np.arange(10).reshape((5, 2)), range(5) X_train, X_t...
stackoverflow.com
https://stackoverflow.com/questions/52908885/random-state-parameter-in-sklearns-train-test-split
random_state parameter in sklearn's train_test_split
What difference does different values of random state makes to the output? For instance, if I set 0 and if I set 100 what difference would it make to the output?
stackoverflow.com
https://stackoverflow.com/questions/52908885/random-state-parameter-in-sklearns-train-test-split
random_state parameter in sklearn's train_test_split
What difference does different values of random state makes to the output? For instance, if I set 0 and if I set 100 what difference would it make to the output?
stackoverflow.com
Housing-Price-Prediction-Project-1/Housing_Price_Prediction pc.ipynb at main · aadityab7/Housing-Price-Prediction-Project-1
This is my first Data Science / Machine Learning Project for Predicting California Housing Price - aadityab7/Housing-Price-Prediction-Project-1
github.com
https://www.geeksforgeeks.org/linear-regression-vs-neural-networks-understanding-key-differences/
Linear Regression vs. Neural Networks: Understanding Key Differences - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
California-Housing-Price-Prediction/California Housing Prices Project-Ransom Kumar.ipynb at main · Ransomk/California-Housing-P
A simple data science project on the California Housing Dataset with some Exploratory data analysis and use of Linear Regression models from sklearn and Seaborn plots - Ransomk/California-Housing-P...
github.com
https://www.geeksforgeeks.org/regression-models-for-california-housing-price-prediction/
Regression Models for California Housing Price Prediction - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
https://phsun102.tistory.com/185
기초 수학 - 데이터 정규화(Data Normalization)
데이터 정규화(Data Normalization)머신 러닝에서 데이터를 학습시키기 전에 데이터들을 정규화(Normalization)해야 한다. 보통 데이터는 특성마다 다른 수의 범위를 가지고 있다. A특성에서는 수의 범위
phsun102.tistory.com
https://phsun102.tistory.com/187
머신 러닝 - IQR 이상치(Outliers) 제거
이상치 제거란?이상치 제거란 데이터셋의 데이터를 분석하는 과정에서 데이터셋 내에 존재하는 이상치(Outliers)를 제거하는 과정을 의미한다. 여기서 이상치란 데이터셋의 데이터가 일정 패턴으
phsun102.tistory.com
'Deep Learning, Machine Learning > Machine Learning' 카테고리의 다른 글
| 머신 러닝 - IQR 이상치(Outliers) 제거 (0) | 2024.08.17 |
|---|

