| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Babel
- mariadb
- Switch
- docker
- linux
- Backbone.js
- Go
- python
- fastapi
- React
- Node
- SQL
- 기초 수학
- webpack
- laravel
- node.js
- Redis
- php
- For
- javascript
- nginx
- Redux
- NCP
- nodejs
- CentOS
- rabbitmq
- Machine Learning
- 블레이드 템플릿
- deep learning
- AWS
- Today
- Total
개발일기
기초 수학 - 델타 논법을 통한 미분 계수 구하기 본문

델타 논법(The Delta Method)이란?
델타 논법은 곡선 위의 어느 지점에서도 경사를 구할 수 있는 방법중 하나다. 쉽게 보면 한 점에서의 경사를 구하는 방법이라고 이해할 수 있다. 두 점의 접점을 점차 가깝게 함으로 한 점의 접점을 그려볼 수 있다. 이를 증명하기 위해 $ y = x^2 + 2{x} + 1 $ 방정식에 임의의 두 점을 그린 후, 두 점 사이의 기울기를 계산해보자.
# Calculate P, Q Slope
import matplotlib.pyplot as plt
import numpy as np
def f(x):
y = x**2 + 2*x + 1 # 방정식
return y
x = np.linspace(-10, 10, 10000) # start, finish, n points
y = f(x) # f(x)
p_y = f(1) # P의 함수값
q_y = f(5) # Q의 함수값
fig, ax = plt.subplots()
plt.axvline(x=0, color='lightgray')
plt.axhline(y=0, color='lightgray')
plt.scatter(1, p_y, c='red', zorder=3) # P
plt.scatter(5, q_y, c='blue', zorder=3) # Q
plt.plot(x, y)
slope_x = [1, 5] # P와 Q의 X값
slope_y = [f(1), f(5)] # P와 Q의 Y값
plt.plot(slope_x, slope_y)
plt.text(1, f(1) +5, 'P (1, ' + str(f(1)) + ')', size=14) # P의 좌표
plt.text(5, f(5) + 5, 'Q (5, ' + str(f(5)) + ')', size=14) # Q의 좌표
plt.show()- zorder: 레이어 순서를 지정한다. zorder를 쓰지 않으면 P, Q가 그래프 뒤에 위치하기 때문에 3으로 지정하였다.
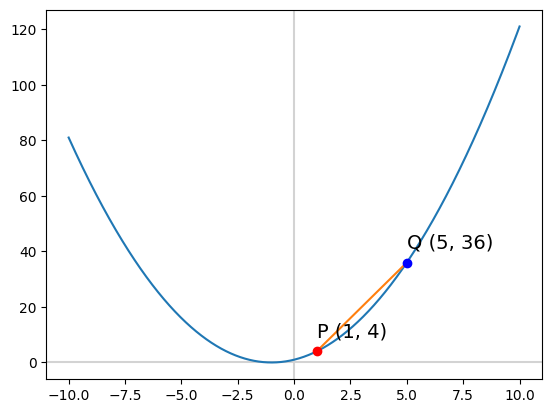
빨간점이 P, 파란점이 Q다. x와 y의 변화율을 바탕으로 두 지점의 기울기를 구할 수 있다.
$ \frac{\text{changei n y}}{\text{changein x}} = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{Q_2 - P_2}{Q_1 - P_1} $ 그리스 문자 델타( $ \Delta $ )를 사용하여 변화율을 표현할 수 있다. 이를 바탕으로 계산하면 $ \frac{\Delta y}{\Delta x} = \frac{36 - 4}{5 - 1} = \frac{32}{4} = 8 $로 계산되며 P와 Q간의 경사는 8이 나온다.
접선(Tangent Line) 그리기
계산한 경사도를 바탕으로 P와 Q의 $ y = ax + b $ 방정식을 계산하여 두 지점을 잇는 직선을 그릴 수 있다.
# P, Q 직선
fig, ax = plt.subplots()
plt.axvline(x=0, color='lightgray')
plt.axhline(y=0, color='lightgray')
plt.scatter(1, p_y, c='red', zorder=3) # P
plt.scatter(5, q_y, c='blue', zorder=3) # Q
plt.plot(x, y)
plt.text(1, f(1) +5, 'P (1, ' + str(f(1)) + ')', size=14) # P의 좌표
plt.text(5, f(5) + 5, 'Q (5, ' + str(f(5)) + ')', size=14) # Q의 좌표
# y = ax + b
a = (36 - 4) / (5 - 1) # 기울기
b = 36 - a*5 # y - ax = b
line_y = a*x + b # P와 Q의 직선
plt.ylim(-5, 130)
plt.plot(x, line_y, c='orange')
plt.show()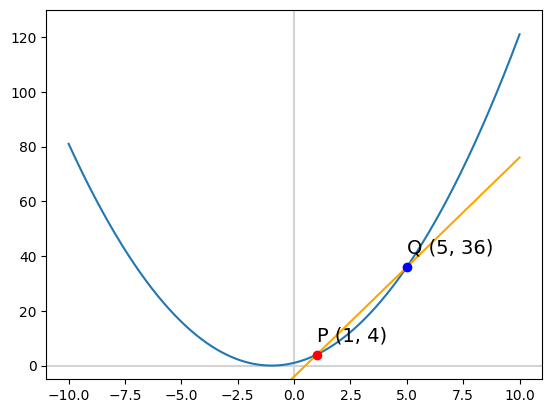
P로의 극한
이제는 두 지점을 점차 가깝게 만들어 나갈 예정이다. P는 그대로 두고 Q의 x값을 1.1로 변경하여 P에 근접하게 만들어 보자. 쉽게 생각하면 $ \displaystyle \lim_{x \to 1}Q_{x, y} $로 Q의 x값이 점차 1의 극한으로 접근한다는 것을 의미한다.
# Q x: 1.1
def get_line_y(p, q):
a = (f(q) - f(p)) / (q - p)
b = f(q) - a * q
y = a*x + b
return y
q_x = 1.1
q_y = f(q_x) # Q의 함수값
fig, ax = plt.subplots()
plt.axvline(x=0, color='lightgray')
plt.axhline(y=0, color='lightgray')
plt.scatter(1, p_y, c='red', zorder=3) # P
plt.scatter(q_x, q_y, c='blue', zorder=4) # Q
plt.ylim(-5, 130)
plt.plot(x, y)
plt.plot(x, get_line_y(1, q_x))
plt.show()빨간점과 파란점이 겹쳐져서 잘 안보이지만 빨간점의 테두리가 은은하게 보이는 것을 확인할 수 있다. P가 1이고 Q가 1.1일때 접선은 위와 같이 나온다.

Q의 x값을 P의 x에 더 근접한 1.000001로 만들어보자
# Q x: 1.000001
def get_line_y(p, q):
a = (f(q) - f(p)) / (q - p)
b = f(q) - a * q
y = a*x + b
return y
q_x = 1.000001
q_y = f(q_x) # Q의 함수값
fig, ax = plt.subplots()
plt.axvline(x=0, color='lightgray')
plt.axhline(y=0, color='lightgray')
plt.scatter(1, p_y, c='red', zorder=3) # P
plt.scatter(q_x, q_y, c='blue', zorder=4) # Q
plt.ylim(-5, 130)
plt.plot(x, y)
plt.plot(x, get_line_y(1, q_x))
plt.show()
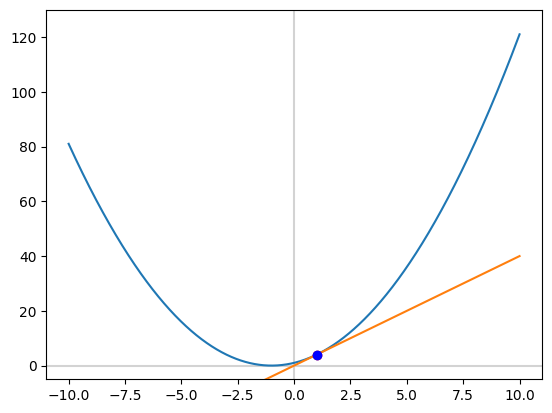
두 점이 거의 완벽하게 겹쳐져 있다. 한점처럼 보이는 이 상태에서 델타 논법을 활용하여 한점의 미분값을 구해낼 수 있다. 공식은 $ \frac{dy}{dx} = \displaystyle \lim_{\Delta x \to 0}\frac{f(x + \Delta x) - f(x)}{\Delta x} $ 이러하다. 거의 근접한 P, Q의 x변화율을 $ \Delta x $에 넣어 미분값을 계산할 수 있다. x변화율은 Q의 x값에서 P의 x값을 뺀것으로 0.000001이 된다. 수학 공식으로 보면 $ \displaystyle \lim_{\Delta x \to 1}\frac{f(x + \Delta x) - f(x)}{\Delta x} = \displaystyle \lim_{\Delta x \to 1}\frac{f(x + 0.000001) - f(x)}{\Delta x} $ 이와 같다. 이를 파이썬 코드에 대입하여 P의 미분값을 구할 수 있다.
# Derivative value
value = (f(1 + 0.000001) - f(1)) / 0.000001
print("Derivative value: ", value)
# 4.000000999759834
미분값 증명
미분값이 제대로 계산되었는지 증명하기 위해 Q의 x값이 1.1이였을 때 x변화율이 0.1인 상황을 대입해보자.
value2 = (f(1 + 0.1) - f(1)) / 0.1
print(value2)
# 4.100000000000001
결과값이 유사하게 나왔으며 1에 극한한다는 것을 고려하면 $ y = x^2 + 2x + 1 $ 방정식에서 x가 1일때 미분값은 4가 된다.
도함수(Derivative) 표기법
델타 논법 공식을 표기할 때 $ \frac{dy}{dx} $라고 표기한 것을 볼 수 있는데 이는 도함수를 의미한다. 미분이랑 도함수는 비슷한 개념인데 도함수는 미분값들을 함수로 일반화시킨 것을 의미한다. 즉 구해진 미분값들을 모두 연결하여 하나의 함수로 나타낸것을 도함수라 지칭한다.
도함수의 표기법은 뉴턴, 라그랑주와 라이츠니츠 표기법이 존재한다.
- 뉴턴 표기법: $ \dot{y} $. $ y $위에 접을 하나 찍는다.
- 라그랑주 표기법: $ f'(x) $. prime기호를 추가한다.
- 라이프니츠 표기법: $ \frac{dy}{dx} $. derivative의 약어인 d를 추가한다.
참고 사이트:
https://www.youtube.com/watch?v=6NlL7Bh1iYo
https://colab.research.google.com/drive/1W90fTwimR8LSqb1R5acsTHp4EK5RaRZA?usp=sharing
Delta Method.ipynb
Colab notebook
colab.research.google.com
'AI > 기초 수학' 카테고리의 다른 글
| 기초 수학 - Pytorch, Tensorflow를 활용한 자동 미분 (0) | 2024.06.24 |
|---|---|
| 기초 수학 - 다양한 미분 법칙 (0) | 2024.06.01 |
| 기초 수학 - 미분(Differential)의 개념 (0) | 2024.05.18 |
| 기초 수학 - PCA(주성분 분석) (0) | 2024.05.01 |
| 기초 수학 - Moore Penrose Pseudo Inverse 유사 역행렬 (0) | 2024.04.21 |




