| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Node
- For
- Go
- node.js
- webpack
- nodejs
- React
- Backbone.js
- python
- rabbitmq
- deep learning
- 블레이드 템플릿
- CentOS
- mariadb
- linux
- laravel
- NCP
- docker
- 기초 수학
- javascript
- Redis
- Redux
- Switch
- SQL
- Machine Learning
- nginx
- AWS
- fastapi
- php
- Babel
- Today
- Total
개발일기
기초 수학 - 미분(Differential)의 개념 본문

미분(Differential)의 기본
미분이란 어느 한 지점의 기울기를 계산하는 것을 의미하며 미분을 통해 함수의 변화율을 구할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, 2, 100)
y = x**2 + 2*x
plt.figure(figsize=(8, 6))
plt.plot(x, y)
plt.plot(-4, 8, 'go') # 초록색 점
plt.plot(-1, -1, 'ro') # 빨간색 점
plt.plot(0, 0, 'yo') # 노란색 점
plt.plot(2, 8, 'bo') # 파란색 점
plt.show()
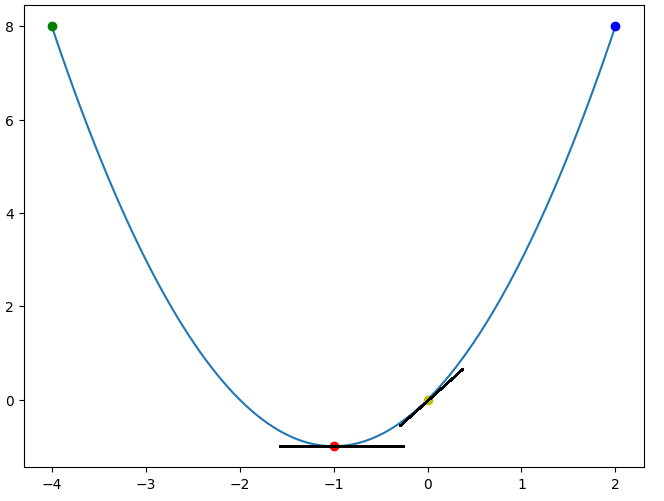
위의 그래프에서 빨간색과 노란색 점에 곡선의 기울기와 일치하는 직선이 그려져 있다. 이 직선은 접선이라 부르며 해당 지점의 기울기를 의미한다. 여기서 기울기란 두 지점 간의 기울어진 정도를 나타내며 수학적으로 보면 $ \frac{y_2 - y_1}{x_2 - x_1} $다. $ y_2 $는 노란색 점의 y값이고 $ y_1 $ 는 빨간색 점의 y값이다. 노란점에서 빨간점으로의 y증가량과 x증가량을 나누면 기울기가 나타나게 된다.
빨간점에서 노란점으로 이동할수록 기울기는 가팔라진다는 것을 알 수 있다. 이와 반대로 초록점에서 빨간점은 기울기가 음수이다. 이를 통해 초록점에서 빨간점으로는 기울기가 완만하게 하강한다는 것을 알 수 있다. 미분이란 이러한 개념을 바탕으로 기울기의 상승 하강을 예측하여 머신러닝 알고리즘 학습을 최적화시키는데 사용된다.
도함수
구해진 미분값으로 새로운 함수를 그려낼 수 있는데 이러한 함수를 도함수라 한다. 도함수는 주어진 함수의 각 지점의 변화율을 계산하여 구해낼 수 있다. 즉 도함수는 해당 함수의 기울기를 나타내며 함수 입력 변수에 따른 함수값의 변화를 나타낸다. 수학에서 기존 함수는 $ f(x) $ 로 표현하지만 도함수는 $ f'(x) $ 로 표현한다. 도함수를 자세하게 알려면 먼저 극한이란 개념을 알고 있어야 한다.
극한(Limit)이란
도함수에서 극한은 함수 변화율을 정의하기 위해 사용하며 특정 값에 한없이 가까워지는 과정을 나타내는 수학적인 개념이다. 즉 $ x=1 $ 이라는 값으로 점점 접근해가는 과정을 극한이라 한다. 극한을 통해 도함수의 순간 변화율을 정의해 나갈 수 있으며 해당 지점의 변화율을 정확하게 구해내기 위해 사용한다. 극한은 $ \displaystyle \lim_{} $ 로 나타내며 아랫첨자를 추가하여 어떤 값으로 가까워지는지 표현할 수 있다. $ \displaystyle \lim_{x \to 0} $ 는 h라는 값이 3으로 한없이 가까워지는 극한을 표현한 것이다. 이러한 극한은 연속 함수에서만 계산되며 이를 토대로 미분은 연속 함수에서만 정의된다.
- 연속 함수(Continuous Function): 함수값과 극한값이 존재하고 이 두 개의 값이 같은 함수
- 불연속 함수(Discontinuous Function): 합수값과 극한값이 존재하지만 이 두 개의 값이 다른 함수. 또는 함수값과 극한값 둘 중 하나가 존재하지 않는 함수

이와 같은게 불연속 함수이다.
극한값(Limit Value) 구하기
극한의 성질을 활용하여 극한값을 구할 수 있다. $ \displaystyle \lim_{x \to 2} x^2 + 2x + 1 $ 의 극한값을 구하려면 x에 2값을 대입하여 계산하면 극한값을 구할 수 있다. x가 2에 가까워지기 때문에 x를 2라고 예상하고 대입하기 때문이다. 그러면 극한값은 9가 나오게 된다. 극한값은 극한이 수렴하는 수에 따라 달라지므로 sympy의 limit메서드를 사용하여 손쉽게 구할 수 있다.
연속함수의 극한값
import sympy
x = Symbol('x') # x를 부호로 지정
y = x**2 + 2*x + 1 # 방정식
a = sympy.limit(y, x, 2) # 극한값 계산
print(a) # 극한값 출력 9Symbol로 x를 부호로 지정한 후, 방정식의 극한값을 구할 수 있다.
symply.limit(y, x, 2): 첫번째는 방정식이 들어있는 변수. 두번째는 극한에 도달하는 변수. 세번째는 극한에 도달하는 변수 x가 어느 지점으로 도달하는지를 나타낸다.
극한값이 제대로 구해졌는지 다음과 같은 코드로 증명해볼 수 있다.
x1 = 1.9999999
x2 = 2.0000001
y1 = x1**2 + 2*x1 + 1
y2 = x2**2 + 2*x2 + 1
print(y1) # 8.99999940000001
print(y2) # 9.000000600000009
2에 수렴하는 값인 x1과 x2값을 방정식에 대입해보니 9와 근사한 값이 나오는 것을 확인할 수 있다.
불연속 함수의 극한값
위에서 본 $ x^2 + 2*x + 1 $ 은 연속 함수이다. 이와 반대로 불연속 함수에서 극한값을 한 번 살펴보자.
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = (x**2 -1) / (x - 1)
plt.plot(x, y)
plt.title(r'$f(x) = \\frac{{x^2 - 1}}{{x - 1}}$')
plt.show()

연속해 보이는 함수지만 x가 1에 극한하면 분모가 0이 되기 때문에 함수값이 정의되지 않는다. 하지만 sympy로 극한값을 구하면 2가 나온다.
from sympy import Symbol, limit
x = sympy.Symbol('x')
y = (x**2 - 1) / (x - 1)
lim = sympy.limit(y, x, 1)
print(lim) # 2
수학적으로 $ \displaystyle \lim_{x \to 1} \frac{ x^2 - 1 }{ x- 1} $ 의 극한값을 구할 때는 인수분해를 사용한다. $ \displaystyle \lim_{x \to 1} \frac{ (x + 1)(x - 1) }{ x- 1} $ 로 인수분해가 한 후, (x - 1)을 약분하면 $ \displaystyle \lim_{x \to 1} x+1 $ 이 남게된다. x에 1을 대입하면 극한값 2가 나온다.
이렇게 보면 인수분해를 하여 함수값을 구할 수 있을것 같다고 생각할 수도 있다. 인수분해는 함수의 형태를 변형하여 계산을 쉽게 할 수 있게 도와주는 것이지 그 자체만으로 함수의 연속성을 판단할 수는 없다. 즉 x가 1일 때 함수값을 구하면 분자와 분모는 모두 0이 되어 함수를 정의할 수 없게 된다. 이 함수는 x가 1인 부분에서 극한값은 존재하지만 함수값이 정의되지 않는 불연속 함수이다.
위와 같이 불연속 함수는 극한값이 존재하는 부분에 흰색 점, 함수값이 존재하는 부분에는 검은 점으로 표시한다.
import matplotlib.pyplot as plt
import numpy as np
import sympy
x = np.linspace(0, 5, 100)
y = (x**2 - 1) / (x - 1)
plt.plot(x, y)
plt.title(r'$lim_{x \\to 1} = \\frac{{x^2 - 1}}{{x - 1}}$')
plt.plot(1, 2, marker='o', color='w', mec='black') # 극한값
plt.show()
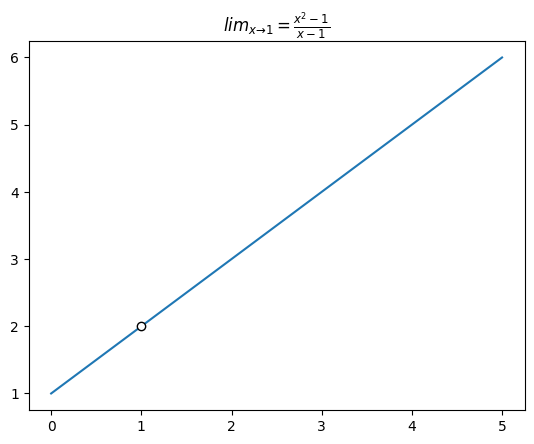
$ \displaystyle \lim_{x \to 1} \frac{ x^2 - 1 }{ x- 1} $ 는 극한값만 존재하기에 흰색점만 찍힌다. 흰색점을 통해 저 부분은 함수값을 정의할 수 없고 극한값만 존재한다는 것을 알려주는 하나의 약속이다.
무한대(Infinity)로의 극한
마지막으로 극한이 무한대로 가는 경우가 존재한다. 이러한 경우는 일반적이며 $ \displaystyle \lim_{ x \to \infty} \frac{5}{x} $ 함수를 예시로 들어 살펴보자. $ \infty $ 는 무한대를 나타내는 수학 기호로 어떠한 수의 끝이 없이 무한히 존재하는 상태를 의미한다.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 400)
y = 5 / x
# 그래프 그리기
plt.plot(x, y, label='y = 5 / x')
plt.title(r'$lim_{x \\to \\infty} = \\frac{5}{x}$')
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.show()

분모 x가 무한대로 극한하므로 함수값은 0일 수가 없으며 0에 최대한 가까워지는 방식으로 그래프가 그려진다. 위 그래프는 왼쪽과 오른쪽을 이어주는 직선이 존재한다. 이 직선이 없는 그래프를 다시 그려보자.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 400)
left_x = x[x<0]
right_x = x[x>0]
left_y = 5 / left_x
right_y = 5 / right_x
plt.plot(left_x, left_y, label='left', color='orange')
plt.plot(right_x, right_y, label='right', color='orange')
plt.title(r'$lim_{x \\to \\infty} = \\frac{5}{x}$')
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.show()

0을 기준으로 왼쪽, 오른쪽 그래프를 따로따로 그리면 가운데 연결되는 직선없이 $ \displaystyle \lim_{ x \to \infty} \frac{5}{x} $ 함수를 시각화 할 수 있다.
참고 사이트:
https://dajeblog.co.kr/https-dajeblog-co-kr-%EB%AF%B8%EB%B6%84/
52. 머신러닝에서 미분의 필요성 - 핵심 이해와 응용 ( feat. 평균변화율 -> 순간변화율 ) - NLP AI
안녕하세요, 다제입니다. 오늘은 머신러닝에서 미분의 중요성을 이해하고, 근본적인 이해부터 실질적인 응용까지 모델을 최적화 방법을 알아보고자해요. 머신러닝의 세계로 여러분을 안내하면
dajeblog.co.kr
https://studywithdavid.tistory.com/13
[하루 5분 수학이야기] 중학생도 이해할 수 있는 짧은 미분 개념 설명
수학을 배워보셨다면 미분이라는 단어는 무조건 들어보셨을 겁니다 하지만 되게 어려워 보이고 글을 읽어봐도 무슨 소리인지 도통 모르겠다 하시는 분들이 계실거라 생각합니다 그래서 아래와
studywithdavid.tistory.com
https://towardsai.net/p/machine-learning/mastering-derivatives-for-machine-learning
Mastering Derivatives for Machine Learning
Originally published on Towards AI. Understanding the building blocks of machine learning. Photo by Michael Dziedzic on Unsplash Author(s): Pratik Shukla “Education is the movement from darkness to light” — Allan BloomTable of Contents: The Slope
towardsai.net
https://medium.com/swlh/fixing-sympys-limit-calculation-flaws-5b46440f97c1
Fixing SymPy’s Limit Calculator Flaw
SymPy is a math Python library that has a flawed limit calculator, this tutorial will cover what a limit is, its flaws, and writing a fix
medium.com
https://colab.research.google.com/drive/1st-_kG0KqNe9j6U1PY9s-jDS5HztgXkM?usp=sharing
미분 기초 - 극한.ipynb
Colab notebook
colab.research.google.com
'AI > 기초 수학' 카테고리의 다른 글
| 기초 수학 - 다양한 미분 법칙 (0) | 2024.06.01 |
|---|---|
| 기초 수학 - 델타 논법을 통한 미분 계수 구하기 (0) | 2024.05.26 |
| 기초 수학 - PCA(주성분 분석) (0) | 2024.05.01 |
| 기초 수학 - Moore Penrose Pseudo Inverse 유사 역행렬 (0) | 2024.04.21 |
| 기초 수학 - 특이값 분해(SVD)를 활용한 이미지 압축 (0) | 2024.04.20 |




